Which table represents an exponential function of the form y=bx when 0
Question

Answer:
The table that represents an exponential function of the form y = [tex]b^{x}[/tex] when 0 < b < 1 is Table - 2. See the attached tables.What is an exponential function?A function is exponential when its value is a constant that is raised to the power of the argument. This is so especially when the function of the constant is e.What is the solution?Recall that the exponential function y = [tex]b^{x}[/tex] given that 0 < b < 1. Notice that the table number 2 see to the exponential function that has the following form:y(x) = (1/3)ˣsubstituting the values of x into the equation, we have:
y(-3) = (1/3) ⁻³ = 27x = -2; thusy(-2) = (1/3) ⁻³ = 9x = -1; thusy(-1) = (1/3) ⁻³ = 3x = 0; thusy(0) = (1/3) ⁻⁰ = 1x = 1; thusy(1) = (1/3) ¹ = 1/3x = 2; thusy(2) = (1/3) ⁻² = 1/9x = 3; thusy(3) = (1/3) ⁻³ = 1/27Therefore, according to the obtained values, one can summarize that the table that depicts the exponential function y = bˣ is table 2.learn more bout exponential functions at:

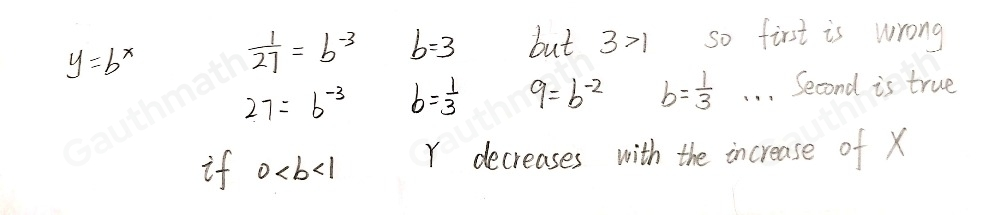
solved
algebra
10 months ago
8796